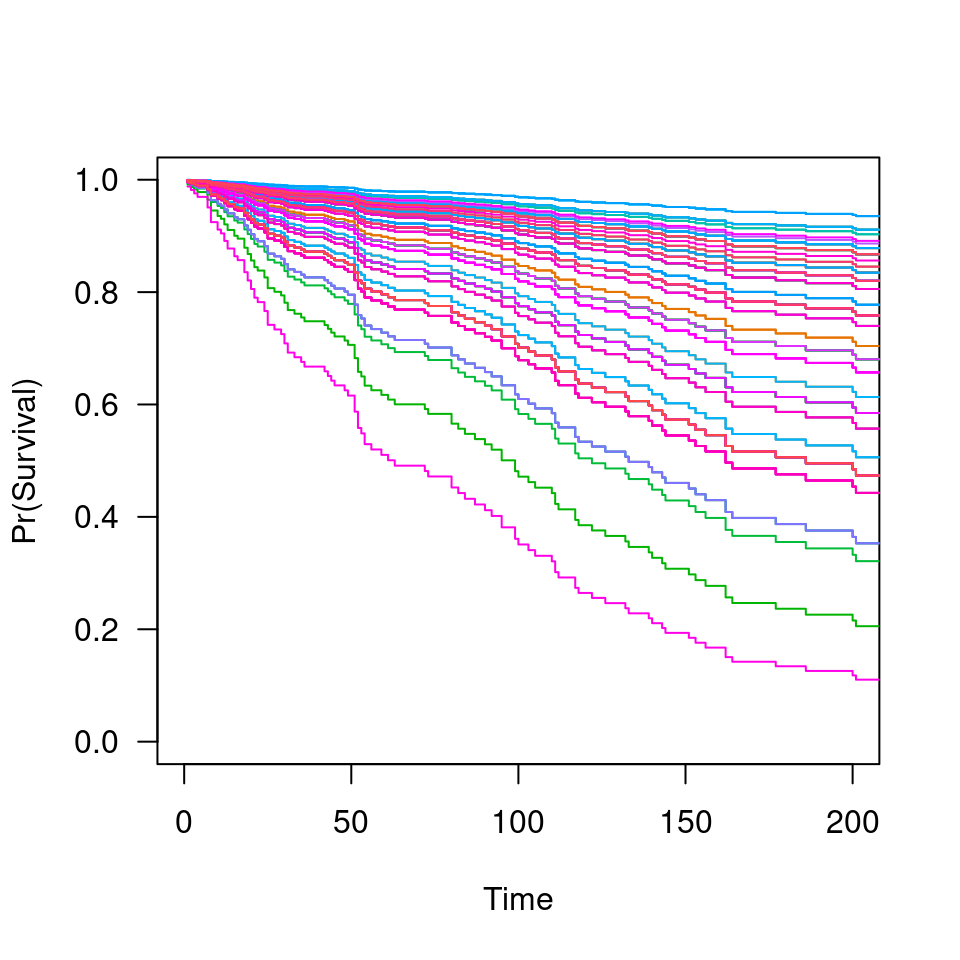
Fit coefficients paths for MCP- or SCAD-penalized Cox regression models over a grid of values for the regularization parameter lambda, with option for an additional L2 penalty.
Arguments
- X
The design matrix of predictor values.
ncvsurvstandardizes the data prior to fitting.- y
The time-to-event outcome, as a two-column matrix or
survival::Surv()object. The first column should be time on study (follow up time); the second column should be a binary variable with 1 indicating that the event has occurred and 0 indicating (right) censoring.- penalty
The penalty to be applied to the model. Either "MCP" (the default), "SCAD", or "lasso".
- gamma
The tuning parameter of the MCP/SCAD penalty (see details). Default is 3 for MCP and 3.7 for SCAD.
- alpha
Tuning parameter for the Mnet estimator which controls the relative contributions from the MCP/SCAD penalty and the ridge, or L2 penalty.
alpha=1is equivalent to MCP/SCAD penalty, whilealpha=0would be equivalent to ridge regression. However,alpha=0is not supported;alphamay be arbitrarily small, but not exactly 0.- lambda.min
The smallest value for lambda, as a fraction of lambda.max. Default is .001 if the number of observations is larger than the number of covariates and .05 otherwise.
- nlambda
The number of lambda values. Default is 100.
- lambda
A user-specified sequence of lambda values. By default, a sequence of values of length
nlambdais computed, equally spaced on the log scale.- eps
Convergence threshhold. The algorithm iterates until the RMSD for the change in linear predictors for any coefficient is less than
eps. Default is1e-4.- max.iter
Maximum number of iterations (total across entire path). Default is 1000.
- convex
Calculate index for which objective function ceases to be locally convex? Default is TRUE.
- dfmax
Upper bound for the number of nonzero coefficients. Default is no upper bound. However, for large data sets, computational burden may be heavy for models with a large number of nonzero coefficients.
- penalty.factor
A multiplicative factor for the penalty applied to each coefficient. If supplied,
penalty.factormust be a numeric vector of length equal to the number of columns ofX. The purpose ofpenalty.factoris to apply differential penalization if some coefficients are thought to be more likely than others to be in the model. In particular,penalty.factorcan be 0, in which case the coefficient is always in the model without any penalization/shrinkage.- warn
Return warning messages for failures to converge and model saturation? Default is TRUE.
- returnX
Return the standardized design matrix along with the fit? By default, this option is turned on if X is under 100 MB, but turned off for larger matrices to preserve memory. Note that certain methods, such as
summary.ncvreg(), require access to the design matrix and may not be able to run ifreturnX=FALSE.- ...
Not used.
Value
An object with S3 class ncvsurv containing:
- beta
The fitted matrix of coefficients. The number of rows is equal to the number of coefficients, and the number of columns is equal to
nlambda.- iter
A vector of length
nlambdacontaining the number of iterations until convergence at each value oflambda.- lambda
The sequence of regularization parameter values in the path.
- penalty, gamma, penalty.factor, alpha, model
Same as above.
- convex.min
The last index for which the objective function is locally convex. The smallest value of lambda for which the objective function is convex is therefore
lambda[convex.min], with corresponding coefficientsbeta[,convex.min].- loss
The deviance of the fitted model at each value of
lambda.- n
The number of instances.
For Cox models, the following objects are also returned (and are necessary to
estimate baseline survival conditonal on the estimated regression
coefficients), all of which are ordered by time on study. I.e., the ith row
of W does not correspond to the ith row of X):
- W
Matrix of
exp(beta)values for each subject over alllambdavalues.- time
Times on study.
- fail
Failure event indicator.
Additionally, if returnX=TRUE, the object will also contain
- X
The standardized design matrix.
Details
The sequence of models indexed by the regularization parameter lambda
is fit using a coordinate descent algorithm. In order to accomplish this,
the second derivative (Hessian) of the Cox partial log-likelihood is
diagonalized (see references for details). The objective function is
defined to be
$$Q(\beta|X, y) = \frac{1}{n} L(\beta|X, y) + P_\lambda(\beta),$$
where the loss function L is the deviance (-2 times the partial
log-likelihood) from the Cox regression mode. See
here for more
details.
Presently, ties are not handled by ncvsurv in a particularly
sophisticated manner. This will be improved upon in a future release of
ncvreg.
References
Breheny P and Huang J. (2011) Coordinate descent algorithms for nonconvex penalized regression, with applications to biological feature selection. Annals of Applied Statistics, 5: 232-253. doi:10.1214/10-AOAS388
Simon N, Friedman JH, Hastie T, and Tibshirani R. (2011) Regularization Paths for Cox's Proportional Hazards Model via Coordinate Descent. Journal of Statistical Software, 39: 1-13. doi:10.18637/jss.v039.i05
See also
Examples
data(Lung)
X <- Lung$X
y <- Lung$y
op <- par(mfrow=c(2,2))
fit <- ncvsurv(X, y)
plot(fit, main=expression(paste(gamma,"=",3)))
fit <- ncvsurv(X, y, gamma=10)
plot(fit, main=expression(paste(gamma,"=",10)))
fit <- ncvsurv(X, y, gamma=1.5)
plot(fit, main=expression(paste(gamma,"=",1.5)))
fit <- ncvsurv(X, y, penalty="SCAD")
plot(fit, main=expression(paste("SCAD, ",gamma,"=",3)))
par(op)
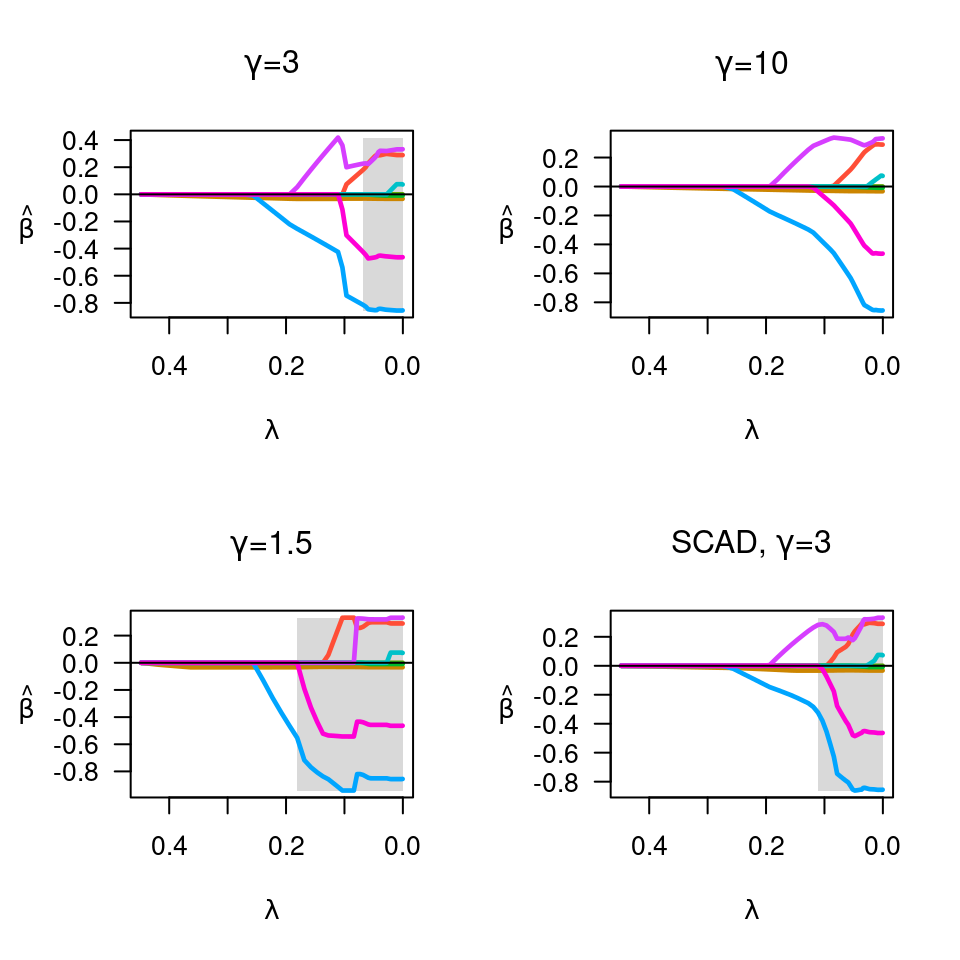
fit <- ncvsurv(X,y)
ll <- log(fit$lambda)
op <- par(mfrow=c(2,1))
plot(ll, BIC(fit), type="l", xlim=rev(range(ll)))
lam <- fit$lambda[which.min(BIC(fit))]
b <- coef(fit, lambda=lam)
b[b!=0]
#> karno squamous adeno
#> -0.03316393 -0.42452397 0.41834812
plot(fit)
abline(v=lam)
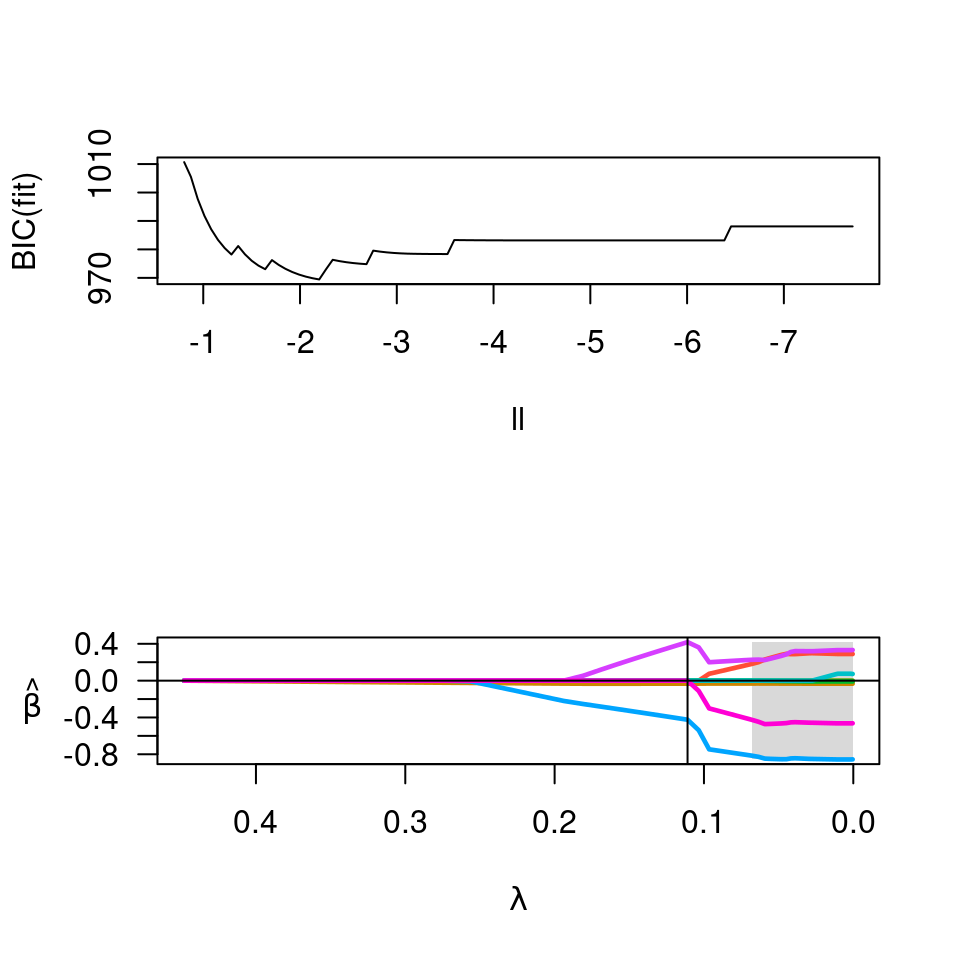par(op)
S <- predict(fit, X, type='survival', lambda=lam)
plot(S, xlim=c(0,200))
