Cross-validation for ncvreg/ncvsurv

Performs k-fold cross validation for MCP- or SCAD-penalized regression models over a grid of values for the regularization parameter lambda.

Usage

cv.ncvreg(
  X,
  y,
  ...,
  cluster,
  nfolds = 10,
  fold,
  returnY = FALSE,
  trace = FALSE
)

cv.ncvsurv(
  X,
  y,
  ...,
  cluster,
  nfolds = 10,
  fold,
  se = c("quick", "bootstrap"),
  returnY = FALSE,
  trace = FALSE
)

Arguments

X: The design matrix, without an intercept, as in ncvreg() or ncvsurv().
y: The response, as in ncvreg() or ncvsurv().
...: Additional arguments to ncvreg() or ncvsurv().
cluster: cv.ncvreg() and cv.ncvsurv() can be run in parallel across a cluster using the parallel package. The cluster must be set up in advance using the parallel::makeCluster() function from that package. The cluster must then be passed to cv.ncvreg() or cv.ncvsurv() (see example).
nfolds: The number of cross-validation folds. Default is 10.
fold: Which fold each observation belongs to. By default the observations are randomly assigned.
returnY: Should cv.ncvreg()/cv.ncvsurv() return the linear predictors from the cross-validation folds? Default is FALSE; if TRUE, this will return a matrix in which the element for row i, column j is the fitted value for observation i from the fold in which observation i was excluded from the fit, at the jth value of lambda. NOTE: For cv.ncvsurv(), the rows of Y are ordered by time on study, and therefore will not correspond to the original order of observations pased to cv.ncvsurv().
trace: If set to TRUE, inform the user of progress by announcing the beginning of each CV fold. Default is FALSE.
se: For cv.ncvsurv(), the method by which the cross-valiation standard error (CVSE) is calculated. The 'quick' approach is based on a rough approximation, but can be calculated more or less instantly. The 'bootstrap' approach is more accurate, but requires additional computing time.

Value

An object with S3 class cv.ncvreg or cv.ncvsurv containing:

cve: The error for each value of lambda, averaged across the cross- validation folds.
cvse: The estimated standard error associated with each value of for cve.
fold: The fold assignments for cross-validation for each observation; note that for cv.ncvsurv(), these are in terms of the ordered observations, not the original observations.
lambda: The sequence of regularization parameter values along which the cross-validation error was calculated.
fit: The fitted ncvreg() or ncvsurv() object for the whole data.
min: The index of lambda corresponding to lambda.min.
lambda.min: The value of lambda with the minimum cross-validation error.
null.dev: The deviance for the intercept-only model. If you have supplied your own lambda sequence, this quantity may not be meaningful.
Bias: The estimated bias of the minimum cross-validation error, as in Tibshirani and Tibshirani (2009) doi:10.1214/08-AOAS224
pe: If family="binomial", the cross-validation prediction error for each value of lambda.
Y: If returnY=TRUE, the matrix of cross-validated fitted values (see above).

Details

The function calls ncvreg/ncvsurv nfolds times, each time leaving out 1/nfolds of the data. The cross-validation error is based on the deviance; see here for more details.

For family="binomial" models, the cross-validation fold assignments are balanced across the 0/1 outcomes, so that each fold has the same proportion of 0/1 outcomes (or as close to the same proportion as it is possible to achieve if cases do not divide evenly).

For Cox models, cv.ncvsurv() uses the approach of calculating the full Cox partial likelihood using the cross-validated set of linear predictors. Other approaches to cross-validation for the Cox regression model have been proposed in the literature; the strengths and weaknesses of the various methods for penalized regression in the Cox model are the subject of current research. A simple approximation to the standard error is provided, although an option to bootstrap the standard error (se='bootstrap') is also available.

References

Breheny P and Huang J. (2011) Coordinate descent algorithms for nonconvex penalized regression, with applications to biological feature selection. Annals of Applied Statistics, 5: 232-253. doi:10.1214/10-AOAS388

Author

Patrick Breheny; Grant Brown helped with the parallelization support

Examples

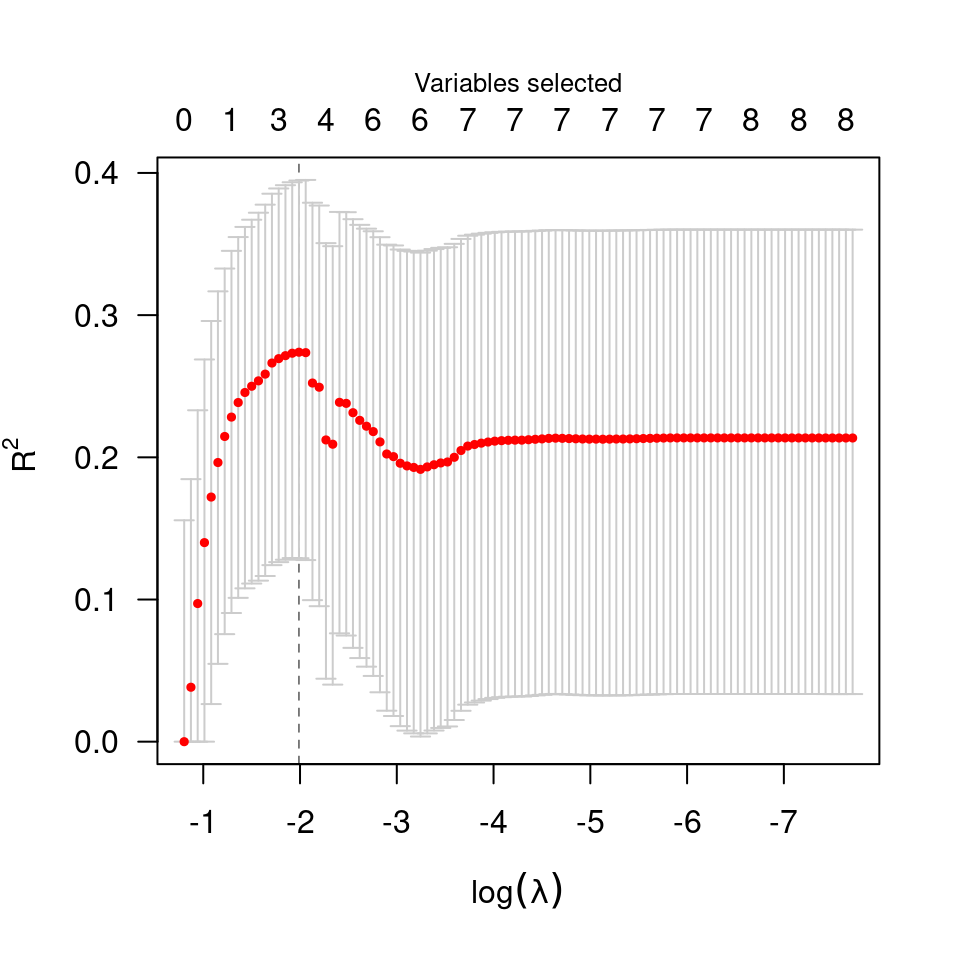
data(Prostate)

cvfit <- cv.ncvreg(Prostate$X, Prostate$y)
plot(cvfit)

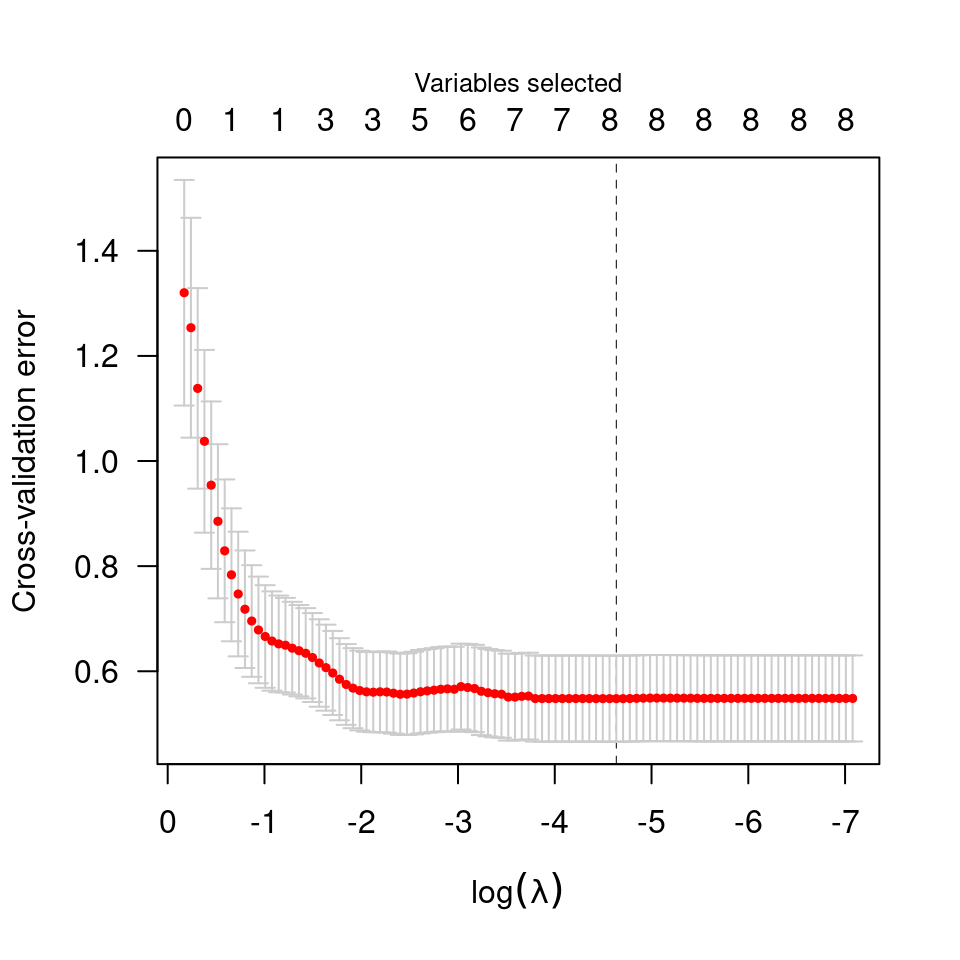summary(cvfit)
#> MCP-penalized linear regression with n=97, p=8
#> At minimum cross-validation error (lambda=0.0068):
#> -------------------------------------------------
#>   Nonzero coefficients: 8
#>   Cross-validation error (deviance): 0.56
#>   R-squared: 0.58
#>   Signal-to-noise ratio: 1.37
#>   Scale estimate (sigma): 0.746
#> MCP-penalized linear regression with n=97, p=8
#> At lambda=0.0068:
#> -------------------------------------------------
#>   Nonzero coefficients         :   8
#>   Expected nonzero coefficients:   3.91
#>   Average mfdr (8 features)    :   0.489
#> 
#>          Estimate      z      mfdr Selected
#> lcavol   0.564342  8.739   < 1e-04        *
#> svi      0.761671  4.143 0.0038898        *
#> lweight  0.622019  3.501 0.0384138        *
#> age     -0.021248 -2.078 0.6572972        *
#> lcp     -0.106050 -1.948 0.7133458        *
#> lbph     0.096712  1.843 0.7519900        *
#> pgg45    0.004458  1.652 0.8089089        *
#> gleason  0.049226  0.467 0.9368023        *

fit <- cvfit$fit
plot(fit)

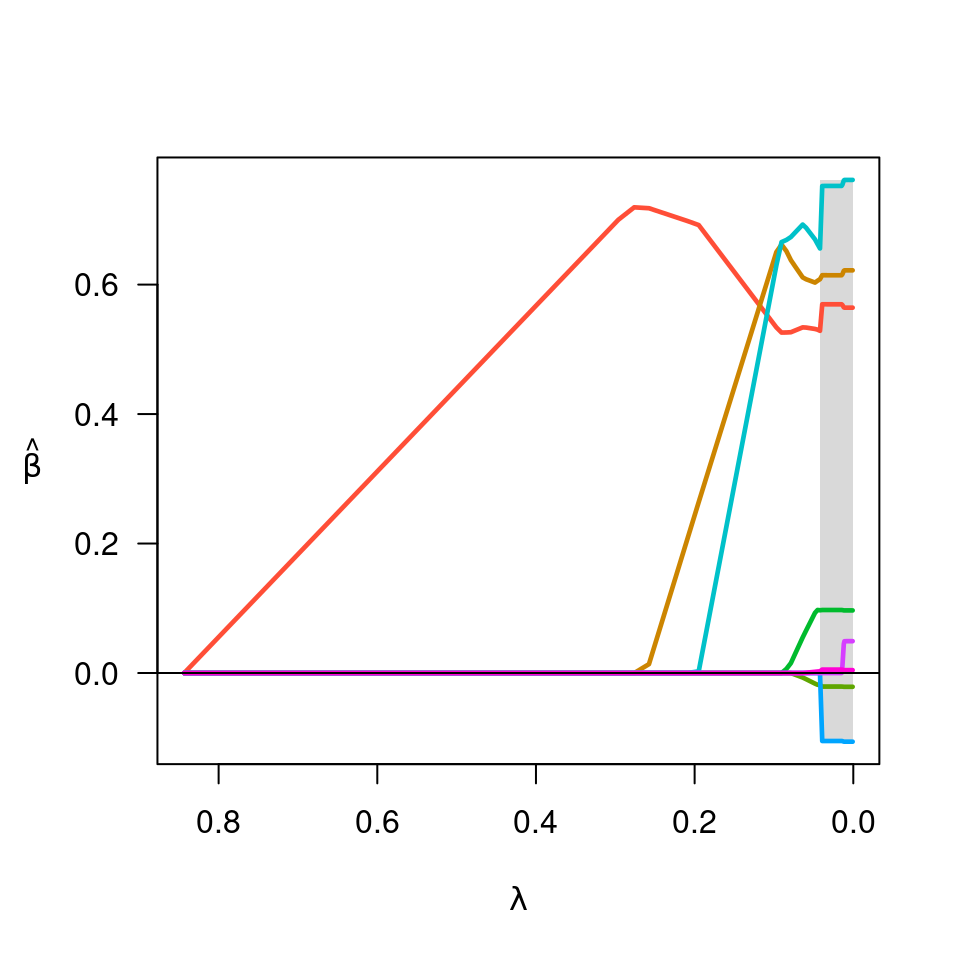beta <- fit$beta[,cvfit$min]

## requires loading the parallel package
if (FALSE) { # \dontrun{
library(parallel)
X <- Prostate$X
y <- Prostate$y
cl <- makeCluster(4)
cvfit <- cv.ncvreg(X, y, cluster=cl, nfolds=length(y))} # }

# Survival
data(Lung)
X <- Lung$X
y <- Lung$y

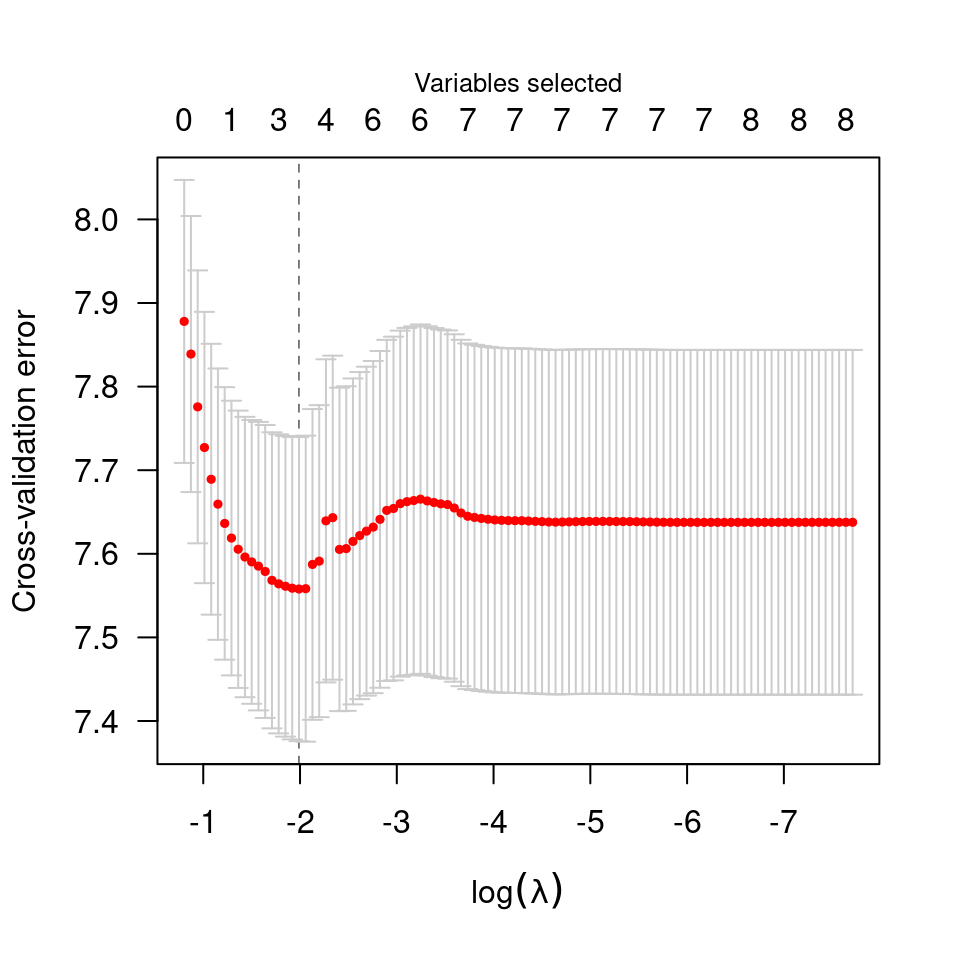
cvfit <- cv.ncvsurv(X, y)
summary(cvfit)
#> MCP-penalized Cox regression with n=137, p=8
#> At minimum cross-validation error (lambda=0.1687):
#> -------------------------------------------------
#>   Nonzero coefficients: 3
#>   Cross-validation error (deviance): 7.55
#>   R-squared: 0.28
#>   Signal-to-noise ratio: 0.39
#> MCP-penalized Cox regression with n=137, p=8
#> At lambda=0.1687:
#> -------------------------------------------------
#>   Nonzero coefficients         :   3
#>   Expected nonzero coefficients:   0.76
#>   Average mfdr (3 features)    :   0.253
#> 
#>          Estimate      z    mfdr Selected
#> karno    -0.03324 -6.555 < 1e-04        *
#> squamous -0.28295 -2.920 0.32331        *
#> adeno     0.12083  2.750 0.43678        *
plot(cvfit)

plot(cvfit, type="rsq")