Extend lasso model fitting to big data that cannot be loaded into memory. Fit solution paths for linear, logistic or Cox regression models penalized by lasso, ridge, or elastic-net over a grid of values for the regularization parameter lambda.
Usage
biglasso(
X,
y,
row.idx = 1:nrow(X),
penalty = c("lasso", "ridge", "enet"),
family = c("gaussian", "binomial", "cox", "mgaussian"),
alg.logistic = c("Newton", "MM"),
screen = c("Adaptive", "SSR", "Hybrid", "None"),
safe.thresh = 0,
update.thresh = 1,
ncores = 1,
alpha = 1,
lambda.min = ifelse(nrow(X) > ncol(X), 0.001, 0.05),
nlambda = 100,
lambda.log.scale = TRUE,
lambda,
eps = 1e-07,
max.iter = 1000,
dfmax = ncol(X) + 1,
penalty.factor = rep(1, ncol(X)),
warn = TRUE,
output.time = FALSE,
return.time = TRUE,
verbose = FALSE
)Arguments
- X
The design matrix, without an intercept. It must be a double type
bigmemory::big.matrix()object. The function standardizes the data and includes an intercept internally by default during the model fitting.- y
The response vector for
family="gaussian"orfamily="binomial". Forfamily="cox",yshould be a two-column matrix with columns 'time' and 'status'. The latter is a binary variable, with '1' indicating death, and '0' indicating right censored. Forfamily="mgaussin",yshould be a n*m matrix where n is the sample size and m is the number of responses.- row.idx
The integer vector of row indices of
Xthat used for fitting the model.1:nrow(X)by default.- penalty
The penalty to be applied to the model. Either
"lasso"(the default),"ridge", or"enet"(elastic net).- family
Either
"gaussian","binomial","cox"or"mgaussian"depending on the response.- alg.logistic
The algorithm used in logistic regression. If "Newton" then the exact hessian is used (default); if "MM" then a majorization-minimization algorithm is used to set an upper-bound on the hessian matrix. This can be faster, particularly in data-larger-than-RAM case.
- screen
The feature screening rule used at each
lambdathat discards features to speed up computation:"SSR"(default ifpenalty="ridge"orpenalty="enet") is the sequential strong rule;"Hybrid", which combines the strong rule with a safe rule."Adaptive"(default forpenalty="lasso"withoutpenalty.factor), which is a variant of Hybrid that avoids recalculating the safe rule when it would not be efficient to do so. Note that: 1. For linear regression with elastic net penalty, both"SSR"and"Hybrid"are applicable since version 1.3-0 2. Only"SSR"is applicable to elastic-net-penalized logistic regression or cox regression 3. Active set cycling is incorporated into all of these screening rules- safe.thresh
the threshold value between 0 and 1 that controls when to stop safe test. For example, 0.01 means to stop safe test at next lambda iteration if the number of features rejected by safe test at current lambda iteration is not larger than 1% of the total number of features. So 1 means to always turn off safe test, whereas 0 (default) means to turn off safe test if the number of features rejected by safe test is 0 at current lambda.
- update.thresh
the non negative threshold value that controls how often to update the reference of safe rules for "Adaptive" methods. Smaller value means updating more often.
- ncores
The number of OpenMP threads used for parallel computing.
- alpha
The elastic-net mixing parameter that controls the relative contribution from the lasso (l1) and the ridge (l2) penalty. The penalty is defined as $$ \alpha||\beta||_1 + (1-\alpha)/2||\beta||_2^2.$$
alpha=1is the lasso penalty,alpha=0the ridge penalty,alphain between 0 and 1 is the elastic-net ("enet") penalty.- lambda.min
The smallest value for lambda, as a fraction of lambda.max. Default is 0.001 if the number of observations is larger than the number of covariates and 0.05 otherwise.
- nlambda
The number of lambda values. Default is 100.
- lambda.log.scale
Whether compute the grid values of lambda on log scale (default) or linear scale.
- lambda
A user-specified sequence of lambda values. By default, a sequence of values of length
nlambdais computed, equally spaced on the log scale.- eps
Convergence threshold for inner coordinate descent. The algorithm iterates until the maximum change in the objective after any coefficient update is less than
epstimes the null deviance. Default value is1e-7.- max.iter
Maximum number of iterations. Default is 1000.
- dfmax
Upper bound for the number of nonzero coefficients. Default is no upper bound. However, for large data sets, computational burden may be heavy for models with a large number of nonzero coefficients.
- penalty.factor
A multiplicative factor for the penalty applied to each coefficient. If supplied,
penalty.factormust be a numeric vector of length equal to the number of columns ofX. The purpose ofpenalty.factoris to apply differential penalization if some coefficients are thought to be more likely than others to be in the model. Currently, the package doesn't allow unpenalized coefficients (penalty.factorcannot be 0).penalty.factoris only supported for "SSR" screen.- warn
Return warning messages for failures to converge and model saturation? Default is TRUE.
- output.time
Whether to print out the start and end time of the model fitting. Default is FALSE.
- return.time
Whether to return the computing time of the model fitting. Default is TRUE.
- verbose
Whether to output the timing of each lambda iteration. Default is FALSE.
Value
An object with S3 class "biglasso" for
"gaussian", "binomial", "cox" families, or an object with S3 class
"mbiglasso" for "mgaussian" family, with following variables.
- beta
The fitted matrix of coefficients, store in sparse matrix representation. The number of rows is equal to the number of coefficients, whereas the number of columns is equal to
nlambda. For"mgaussian"family with m responses, it is a list of m such matrices.- iter
A vector of length
nlambdacontaining the number of iterations until convergence at each value oflambda.- lambda
The sequence of regularization parameter values in the path.
- penalty
Same as above.
- family
Same as above.
- alpha
Same as above.
- loss
A vector containing either the residual sum of squares (for
"gaussian", "mgaussian") or negative log-likelihood (for"binomial", "cox") of the fitted model at each value oflambda.- penalty.factor
Same as above.
- n
The number of observations used in the model fitting. It's equal to
length(row.idx).- center
The sample mean vector of the variables, i.e., column mean of the sub-matrix of
Xused for model fitting.- scale
The sample standard deviation of the variables, i.e., column standard deviation of the sub-matrix of
Xused for model fitting.- y
The response vector used in the model fitting. Depending on
row.idx, it could be a subset of the raw input of the response vector y.- screen
Same as above.
- col.idx
The indices of features that have 'scale' value greater than 1e-6. Features with 'scale' less than 1e-6 are removed from model fitting.
- rejections
The number of features rejected at each value of
lambda.- safe_rejections
The number of features rejected by safe rules at each value of
lambda.
Details
The objective function for linear regression or multiple responses linear regression
(family = "gaussian" or family = "mgaussian") is
$$\frac{1}{2n}\textrm{RSS} + \lambda \cdot \textrm{penalty},$$
where for family = "mgaussian"), a group-lasso type penalty is applied.
For logistic regression
(family = "binomial") it is $$-\frac{1}{n} \ell +
\lambda \cdot \textrm{penalty},$$ for cox regression,
breslow approximation for ties is applied.
Several advanced feature screening rules are implemented. For
lasso-penalized linear regression, all the options of screen are
applicable. Our proposal adaptive rule - "Adaptive" - achieves highest speedup
so it's the recommended one, especially for ultrahigh-dimensional large-scale
data sets. For cox regression and/or the elastic net penalty, only
"SSR" is applicable for now. More efficient rules are under development.
References
Zeng Y and Breheny P. (2021) The biglasso Package: A Memory- and Computation- Efficient Solver for Lasso Model Fitting with Big Data in R. R Journal, 12: 6-19. doi:10.32614/RJ-2021-001
Examples
## Linear regression
data(colon)
X <- colon$X
y <- colon$y
x_bm <- as.big.matrix(X)
# lasso, default
fit_lasso <- biglasso(x_bm, y, family = "gaussian")
plot(fit_lasso, log.l = TRUE, main = "lasso")
 # elastic net
fit_enet <- biglasso(x_bm, y, penalty = 'enet', alpha = 0.5, family = 'gaussian')
plot(fit_enet, log.l = TRUE, main = 'elastic net')
# elastic net
fit_enet <- biglasso(x_bm, y, penalty = 'enet', alpha = 0.5, family = 'gaussian')
plot(fit_enet, log.l = TRUE, main = 'elastic net')
 ## Logistic regression
fit_bin_lasso <- biglasso(x_bm, y, penalty = 'lasso', family = "binomial")
plot(fit_bin_lasso, log.l = TRUE, main = 'lasso')
## Logistic regression
fit_bin_lasso <- biglasso(x_bm, y, penalty = 'lasso', family = "binomial")
plot(fit_bin_lasso, log.l = TRUE, main = 'lasso')
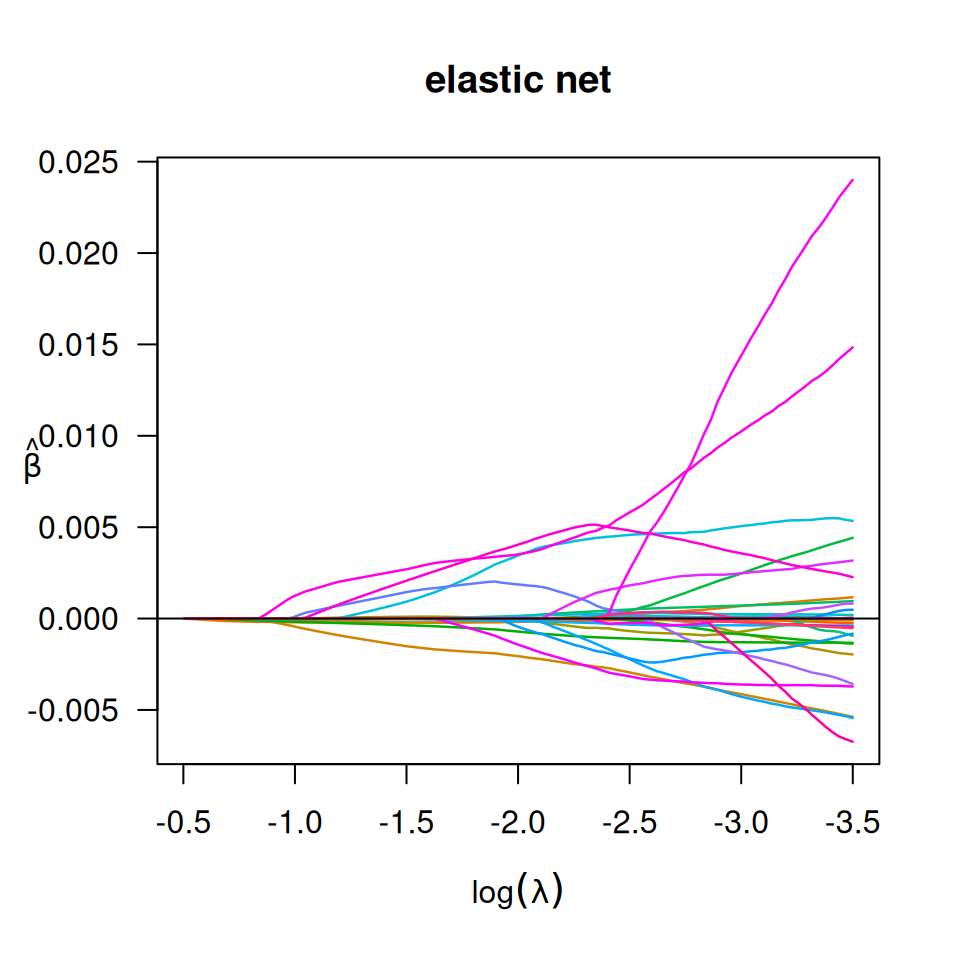
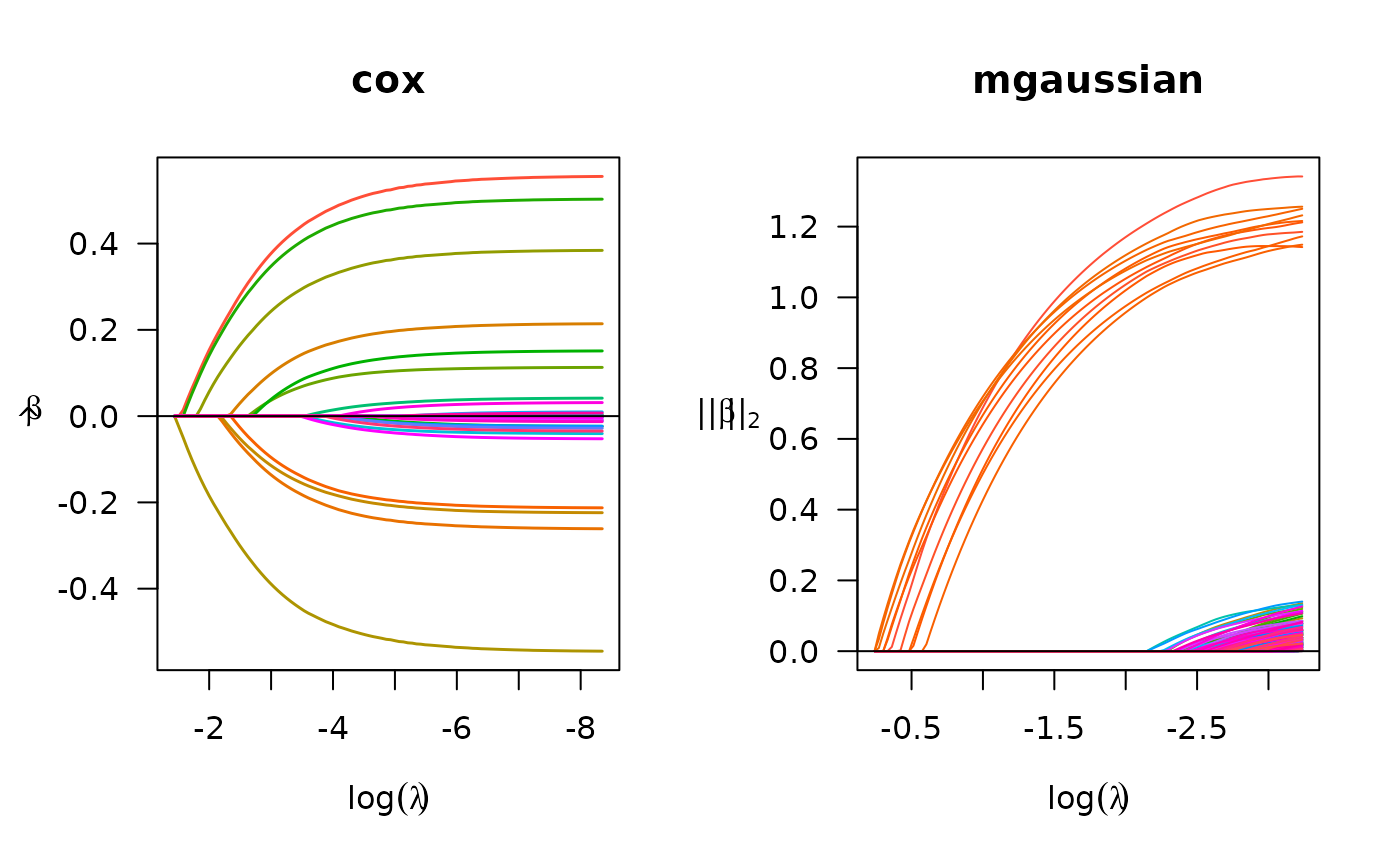 # elastic net
fit_bin_enet <- biglasso(x_bm, y, penalty = 'enet', alpha = 0.5, family = "binomial")
plot(fit_bin_enet, log.l = TRUE, main = 'elastic net')
# elastic net
fit_bin_enet <- biglasso(x_bm, y, penalty = 'enet', alpha = 0.5, family = "binomial")
plot(fit_bin_enet, log.l = TRUE, main = 'elastic net')
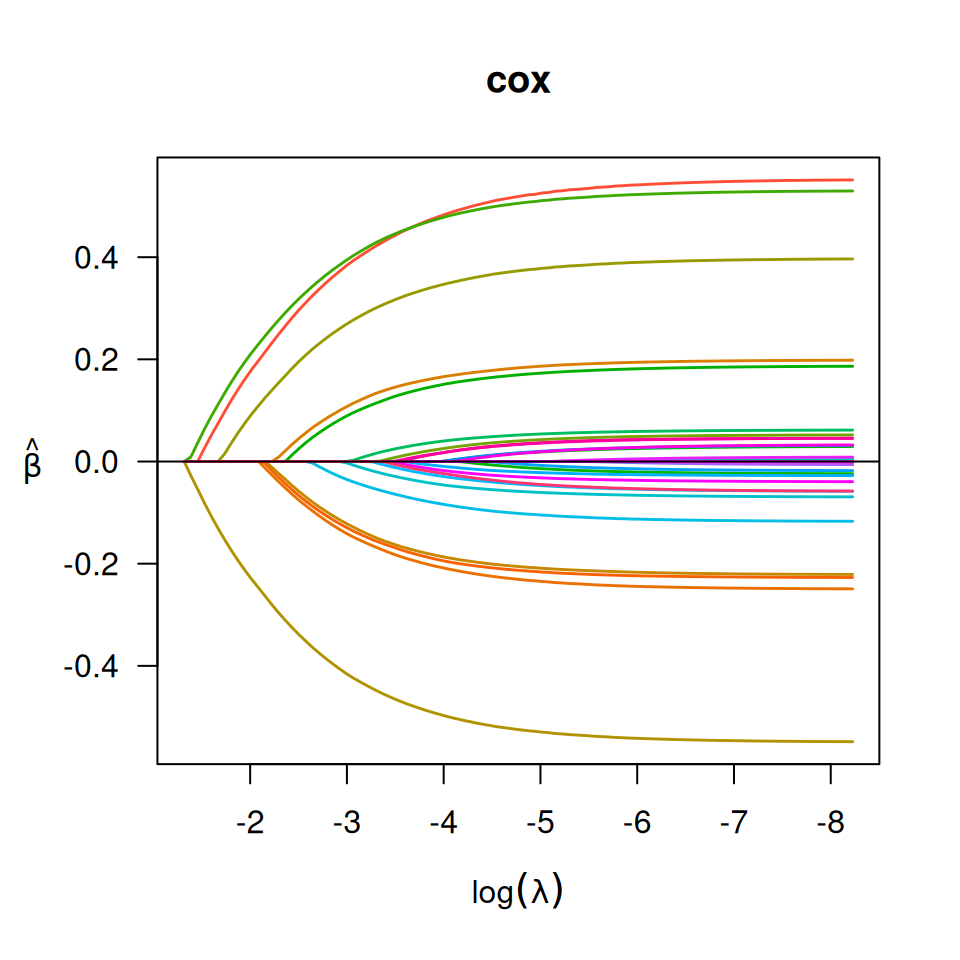
 ## Cox regression
set.seed(10101)
n <- 1000
p <- 30
nzc <- p / 3
x <- matrix(rnorm(n * p), n, p)
beta <- rnorm(nzc)
fx <- x[, seq(nzc)] %*% beta/3
hx <- exp(fx)
ty <- rexp(n, hx)
tcens <- quantile(ty, 0.7)
y <- cbind(time = pmin(ty, tcens), status = ty < tcens)
x_bm <- as.big.matrix(x)
fit <- biglasso(x_bm, y, family = "cox")
plot(fit, main = "cox")
## Cox regression
set.seed(10101)
n <- 1000
p <- 30
nzc <- p / 3
x <- matrix(rnorm(n * p), n, p)
beta <- rnorm(nzc)
fx <- x[, seq(nzc)] %*% beta/3
hx <- exp(fx)
ty <- rexp(n, hx)
tcens <- quantile(ty, 0.7)
y <- cbind(time = pmin(ty, tcens), status = ty < tcens)
x_bm <- as.big.matrix(x)
fit <- biglasso(x_bm, y, family = "cox")
plot(fit, main = "cox")
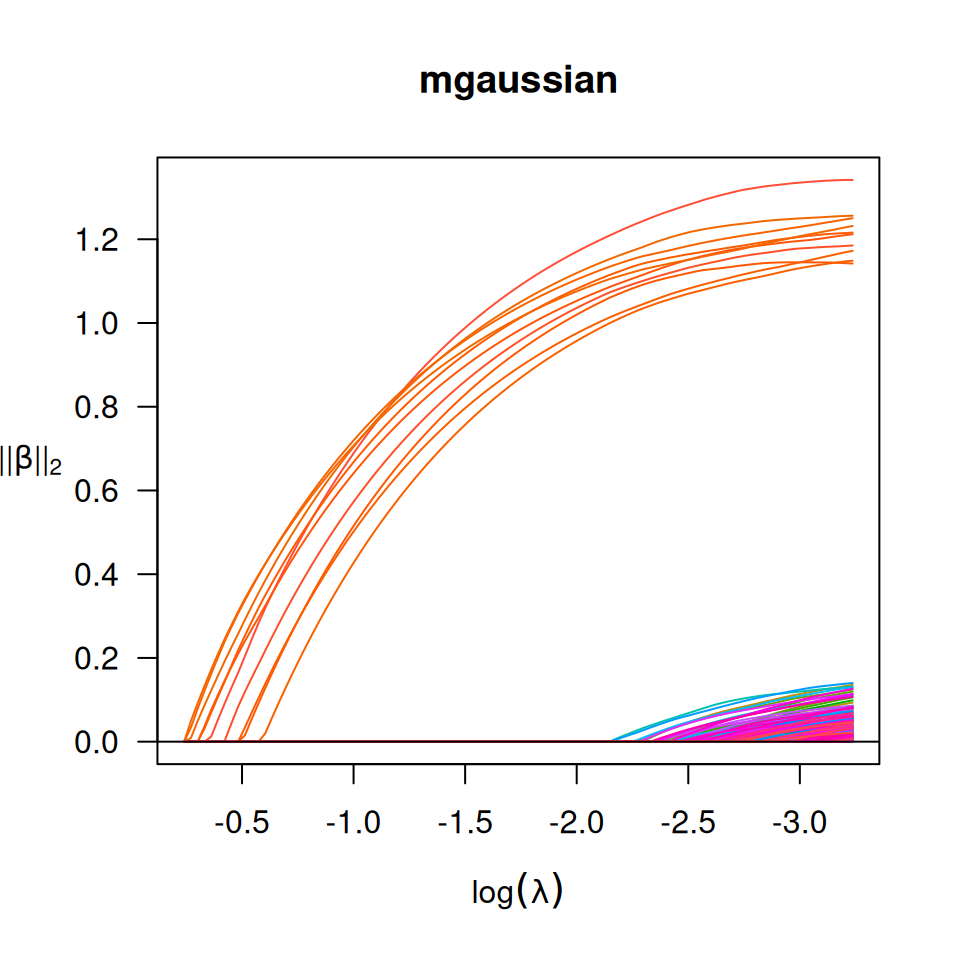
 ## Multiple responses linear regression
set.seed(10101)
n <- 300
p <- 300
m <- 5
s <- 10
b <- 1
x <- matrix(rnorm(n * p), n, p)
beta <- matrix(seq(from = -b, to = b, length.out = s * m), s, m)
y = x[, 1:s] %*% beta + matrix(rnorm(n * m, 0, 1), n, m)
x_bm = as.big.matrix(x)
fit = biglasso(x_bm, y, family = "mgaussian")
plot(fit, main = "mgaussian")
## Multiple responses linear regression
set.seed(10101)
n <- 300
p <- 300
m <- 5
s <- 10
b <- 1
x <- matrix(rnorm(n * p), n, p)
beta <- matrix(seq(from = -b, to = b, length.out = s * m), s, m)
y = x[, 1:s] %*% beta + matrix(rnorm(n * m, 0, 1), n, m)
x_bm = as.big.matrix(x)
fit = biglasso(x_bm, y, family = "mgaussian")
plot(fit, main = "mgaussian")