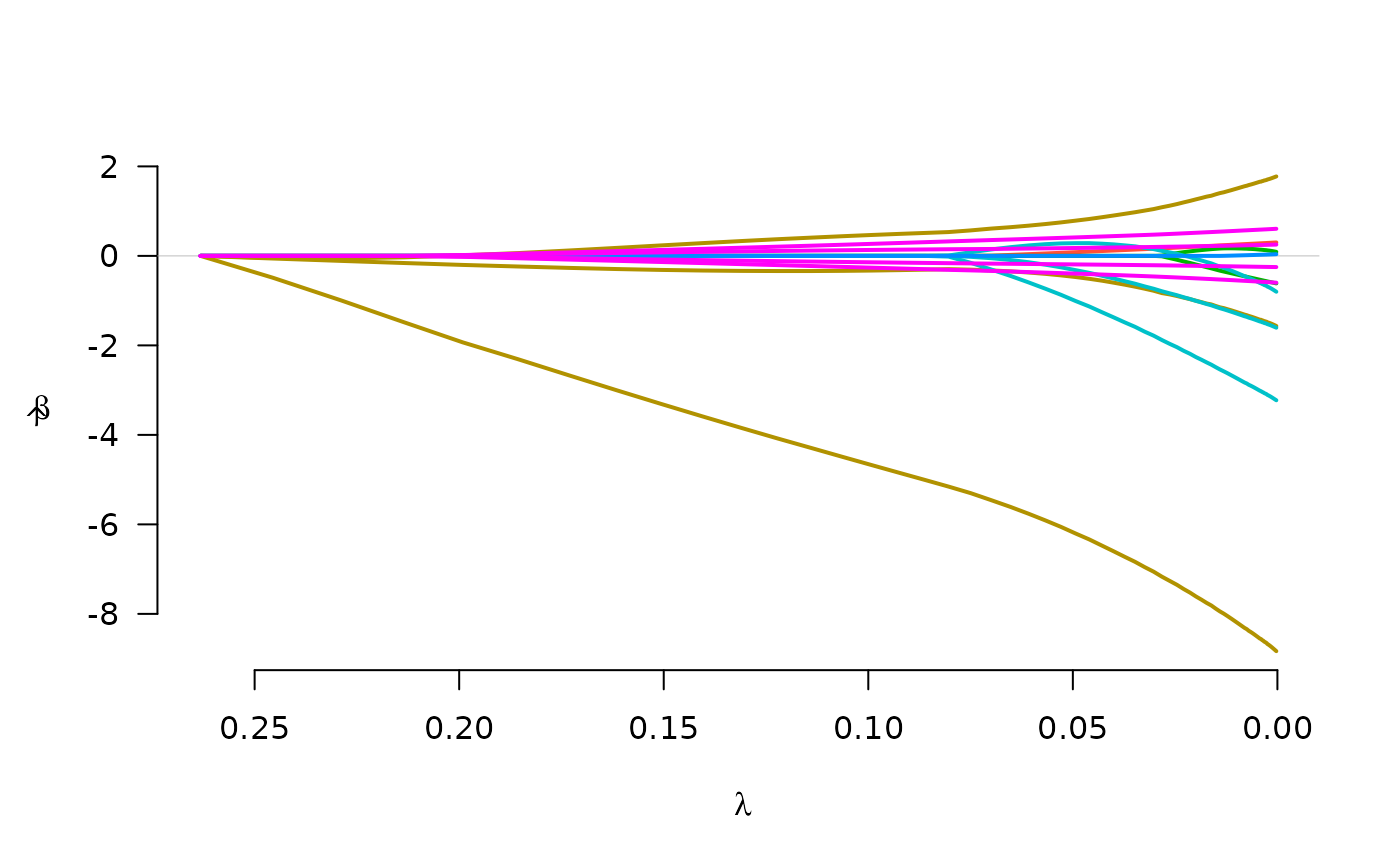
Fit an group penalized survival model

Fit regularization paths for Cox models with grouped penalties over a grid of values for the regularization parameter lambda.

Usage

grpsurv(
  X,
  y,
  group = 1:ncol(X),
  penalty = c("grLasso", "grMCP", "grSCAD", "gel", "cMCP"),
  gamma = ifelse(penalty == "grSCAD", 4, 3),
  alpha = 1,
  nlambda = 100,
  lambda,
  lambda.min = {
     if (nrow(X) > ncol(X)) 
         0.001
     else 0.05
 },
  eps = 0.001,
  max.iter = 10000,
  dfmax = p,
  gmax = length(unique(group)),
  tau = 1/3,
  group.multiplier,
  warn = TRUE,
  returnX = FALSE,
  ...
)

Arguments

X: The design matrix.
y: The time-to-event outcome, as a two-column matrix or Surv object. The first column should be time on study (follow up time); the second column should be a binary variable with 1 indicating that the event has occurred and 0 indicating (right) censoring.
group: A vector describing the grouping of the coefficients. For greatest efficiency and least ambiguity (see details), it is best if group is a factor or vector of consecutive integers, although unordered groups and character vectors are also allowed. If there are coefficients to be included in the model without being penalized, assign them to group 0 (or "0").
penalty: The penalty to be applied to the model. For group selection, one of grLasso, grMCP, or grSCAD. For bi-level selection, one of gel or cMCP. See below for details.
gamma: Tuning parameter of the group or composite MCP/SCAD penalty (see details). Default is 3 for MCP and 4 for SCAD.
alpha: grpsurv allows for both a group penalty and an L2 (ridge) penalty; alpha controls the proportional weight of the regularization parameters of these two penalties. The group penalties' regularization parameter is lambda*alpha, while the regularization parameter of the ridge penalty is lambda*(1-alpha). Default is 1: no ridge penalty.
nlambda: The number of lambda values. Default is 100.
lambda: A user-specified sequence of lambda values. By default, a sequence of values of length nlambda is computed automatically, equally spaced on the log scale.
lambda.min: The smallest value for lambda, as a fraction of lambda.max. Default is .001 if the number of observations is larger than the number of covariates and .05 otherwise.
eps: Convergence threshhold. The algorithm iterates until the RMSD for the change in linear predictors for each coefficient is less than eps. Default is 0.001.
max.iter: Maximum number of iterations (total across entire path). Default is 10000.
dfmax: Limit on the number of parameters allowed to be nonzero. If this limit is exceeded, the algorithm will exit early from the regularization path.
gmax: Limit on the number of groups allowed to have nonzero elements. If this limit is exceeded, the algorithm will exit early from the regularization path.
tau: Tuning parameter for the group exponential lasso; defaults to 1/3.
group.multiplier: A vector of values representing multiplicative factors by which each group's penalty is to be multiplied. Often, this is a function (such as the square root) of the number of predictors in each group. The default is to use the square root of group size for the group selection methods, and a vector of 1's (i.e., no adjustment for group size) for bi-level selection.
warn: Return warning messages for failures to converge and model saturation? Default is TRUE.
returnX: Return the standardized design matrix? Default is FALSE.
...: Not used.

Value

An object with S3 class "grpsurv" containing:

beta: The fitted matrix of coefficients. The number of rows is equal to the number of coefficients, and the number of columns is equal to nlambda.
group: Same as above.
lambda: The sequence of lambda values in the path.
penalty: Same as above.
gamma: Same as above.
alpha: Same as above.
deviance: The deviance of the fitted model at each value of lambda.
n: The number of observations.
df: A vector of length nlambda containing estimates of effective number of model parameters all the points along the regularization path. For details on how this is calculated, see Breheny and Huang (2009).
iter: A vector of length nlambda containing the number of iterations until convergence at each value of lambda.
group.multiplier: A named vector containing the multiplicative constant applied to each group's penalty.

For Cox models, the following objects are also returned (and are necessary to estimate baseline survival conditional on the estimated regression coefficients), all of which are ordered by time on study (i.e., the ith row of W does not correspond to the ith row of X):

W: Matrix of exp(beta) values for each subject over all lambda values.
time: Times on study.
fail: Failure event indicator.

Details

The sequence of models indexed by the regularization parameter lambda is fit using a coordinate descent algorithm. In order to accomplish this, the second derivative (Hessian) of the Cox partial log-likelihood is diagonalized (see references for details). The objective function is defined to be $$Q(\beta|X, y) = \frac{1}{n} L(\beta|X, y) + $$$$ P_\lambda(\beta)$$ where the loss function L is the negative partial log-likelihood (half the deviance) from the Cox regression model. See here for more details.

Presently, ties are not handled by grpsurv in a particularly sophisticated manner. This will be improved upon in a future release of grpreg.

References

Breheny P and Huang J. (2009) Penalized methods for bi-level variable selection. Statistics and its interface, 2: 369-380. doi:10.4310/sii.2009.v2.n3.a10
Huang J, Breheny P, and Ma S. (2012). A selective review of group selection in high dimensional models. Statistical Science, 27: 481-499. doi:10.1214/12-sts392
Breheny P and Huang J. (2015) Group descent algorithms for nonconvex penalized linear and logistic regression models with grouped predictors. Statistics and Computing, 25: 173-187. doi:10.1007/s11222-013-9424-2
Breheny P. (2015) The group exponential lasso for bi-level variable selection. Biometrics, 71: 731-740. doi:10.1111/biom.12300
Simon N, Friedman JH, Hastie T, and Tibshirani R. (2011) Regularization Paths for Cox's Proportional Hazards Model via Coordinate Descent. Journal of Statistical Software, 39: 1-13. doi:10.18637/jss.v039.i05

Author

Patrick Breheny

Examples

data(Lung)
X <- Lung$X
y <- Lung$y
group <- Lung$group

fit <- grpsurv(X, y, group)
plot(fit)


S <- predict(fit, X, type='survival', lambda=0.05)
plot(S, xlim=c(0,200))