Permutation fitting for ncvreg

Fits multiple penalized regression models in which the outcome is randomly permuted, thereby allowing estimation of the marginal false discovery rate.

Usage

perm.ncvreg(
  X,
  y,
  ...,
  permute = c("outcome", "residuals"),
  N = 10,
  seed,
  trace = FALSE
)

Arguments

X

The design matrix, without an intercept, as in ncvreg.

y

The response vector, as in ncvreg.

...

Additional arguments to ncvreg.

permute

What to permute. If 'outcome', the response vector, y, is permuted. If 'residuals', the residuals are permuted. This is only available for linear regression (i.e., for family='gaussian'). Note that permuting the residuals may take a long time, as the residuals differ for each value of lambda, so separate permutations are required at every value of lambda. See also permres().

N

The number of permutation replications. Default is 10.

seed

You may set the seed of the random number generator in order to obtain reproducible results.

trace

If set to TRUE, perm.ncvreg will inform the user of its progress by announcing the beginning of each permutation fit. Default is FALSE.

Value

An object with S3 class "perm.ncvreg" containing:

EF

The number of variables selected at each value of lambda, averaged over the permutation fits.

S

The actual number of selected variables for the non-permuted data.

mFDR

The estimated marginal false discovery rate (EF/S).

fit

The fitted ncvreg object for the original (non-permuted) data.

loss

The loss/deviance for each value of lambda, averaged over the permutation fits. This is an estimate of the explanatory power of the model under null conditions, and can be used to adjust the loss of the fitted model in a manner akin to the idea of an adjusted R-squared in classical regression.

Details

The function fits a penalized regression model to the actual data, then repeats the process N times with a permuted version of the response vector. This allows estimation of the expected number of variables included by chance for each value of lambda. The ratio of this expected quantity to the number of selected variables using the actual (non-permuted) response is called the marginal false discovery rate (mFDR).

See also

ncvreg(), plot.mfdr(), mfdr()

Author

Patrick Breheny patrick-breheny@uiowa.edu

Examples

# Linear regression --------------------------------------------------
data(Prostate)
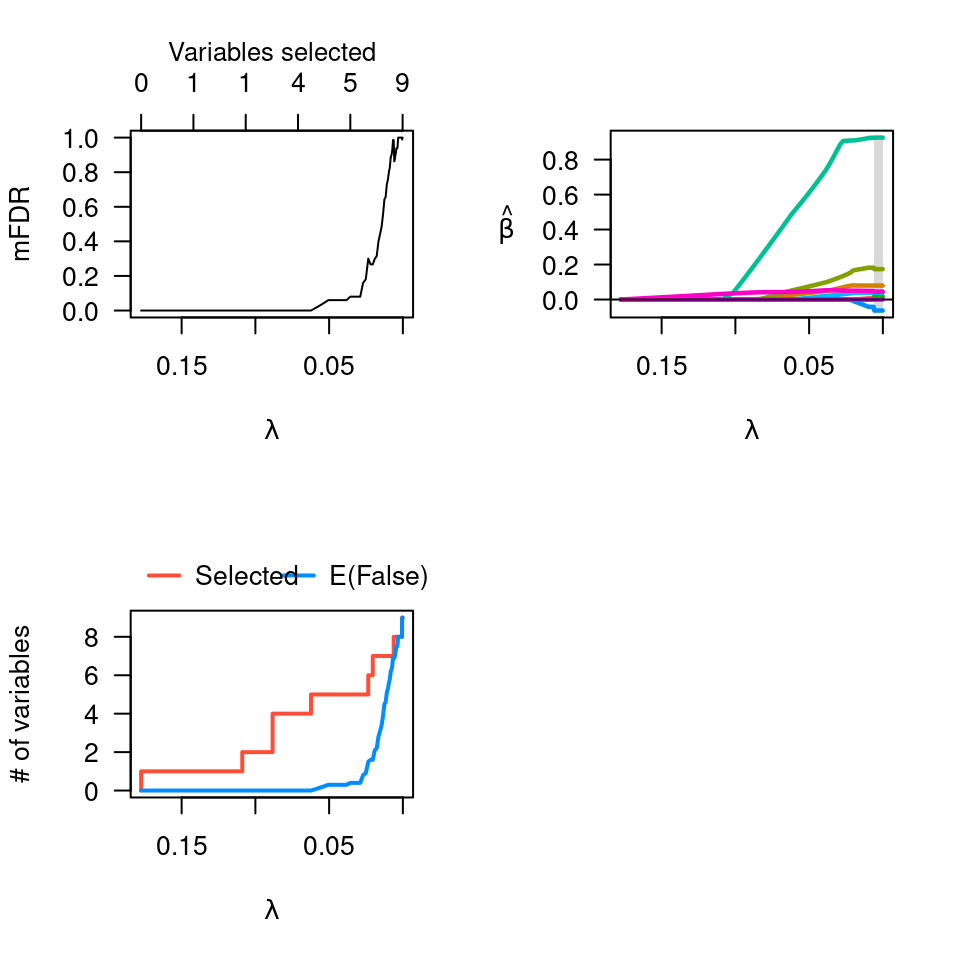
pmfit <- perm.ncvreg(Prostate$X, Prostate$y)

op <- par(mfcol=c(2,2))
plot(pmfit)
plot(pmfit, type="EF")
plot(pmfit$fit)
lam <- pmfit$fit$lambda

pmfit.r <- perm.ncvreg(Prostate$X, Prostate$y, permute='residuals')
plot(pmfit.r, col="red")              # Permuting residuals is
lines(lam, pmfit$mFDR, col="gray60")  # less conservative

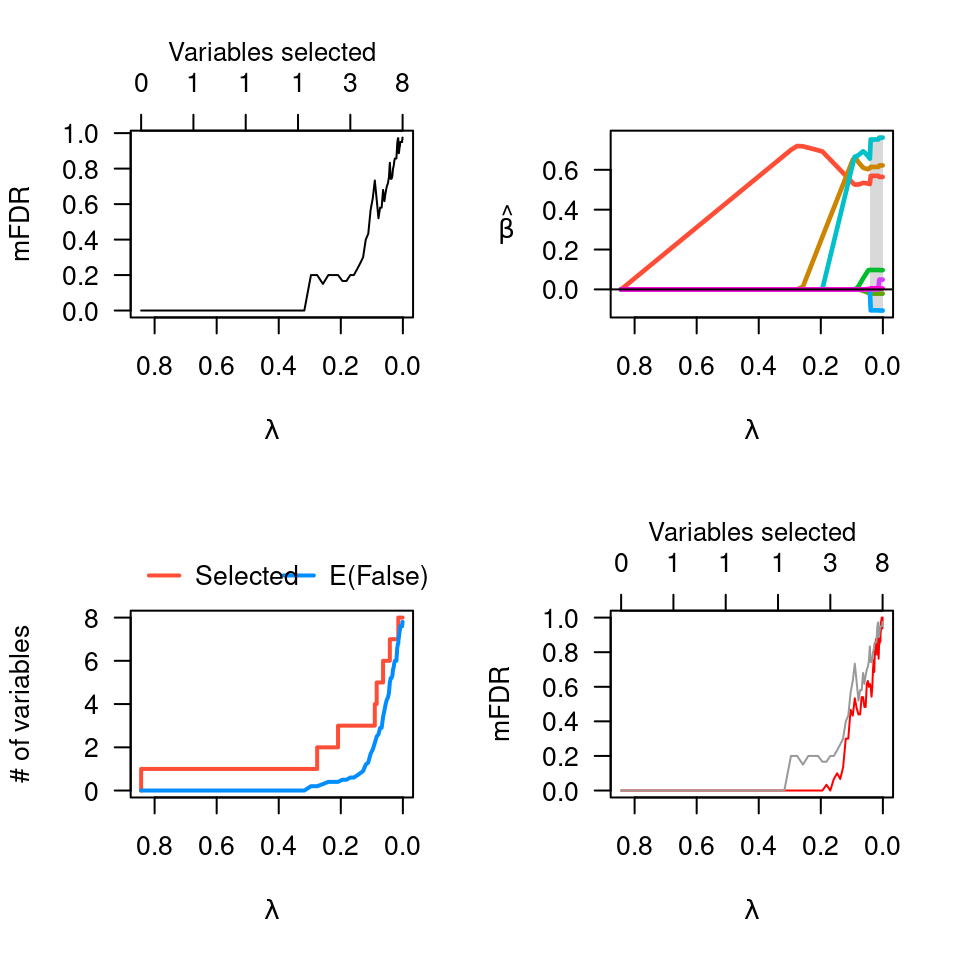par(op)

# Logistic regression ------------------------------------------------
data(Heart)
pmfit <- perm.ncvreg(Heart$X, Heart$y, family="binomial")

op <- par(mfcol=c(2,2))
plot(pmfit)
plot(pmfit, type="EF")
plot(pmfit$fit)
par(op)