If your data is in a matrix or data frame • plmmr

library(plmmr)
#> Loading required package: bigalgebra
#> Loading required package: bigmemory
#> This is version 4.1.1.0 of plmmr.
#> Note: plmmr depends on the package bigalgebra, the current GitHub version of which is throwing some warnings for filebacked analysis.
#> 
#>  https://github.com/fbertran/bigalgebra/issues/2 
#> 
#> If you see a warning about 'stack imbalance' appear while you are fitting a model with plmm() or cv_plmm(), we recommend downloading the last stable version of bigalebra.
#> If you are analyzing data stored in your R session memory, you can disregard this message.

In this overview, I will provide a demo of the main functions in plmmr using the admix data. Checkout the other vignettes to see examples of analyzing data from PLINK files or delimited files.

Examine what we have in the admix data:

str(admix)
#> List of 3
#>  $ X       : int [1:197, 1:100] 0 0 0 0 1 0 1 0 0 0 ...
#>   ..- attr(*, "dimnames")=List of 2
#>   .. ..$ : NULL
#>   .. ..$ : chr [1:100] "Snp1" "Snp2" "Snp3" "Snp4" ...
#>  $ y       : num [1:197, 1] 3.52 3.754 1.191 0.579 4.085 ...
#>  $ ancestry: num [1:197] 1 1 1 1 1 1 1 1 1 1 ...

Basic model fitting

The admix dataset is now ready to analyze with a call to plmmr::plmm() (one of the main functions in plmmr):

admix_fit <- plmm(admix$X, admix$y)
summary(admix_fit, lambda = admix_fit$lambda[50])
#> lasso-penalized regression model with n=197, p=101 at lambda=0.01426
#> -------------------------------------------------
#> The model converged 
#> -------------------------------------------------
#> # of non-zero coefficients:  88 
#> -------------------------------------------------

Notice: I am passing admix$X as the design argument in plmm(); internally, plmm() has taken this X input and created a plmm_design object. You could also supply X and y to create_design() to make this step explicit.

The returned beta_vals item is a matrix whose rows are \hat\beta coefficients and whose columns represent values of the penalization parameter \lambda. By default, plmm fits 100 values of \lambda (see the setup_lambda function for details).

admix_fit$beta_vals[1:10, 97:100] |> 
  knitr::kable(digits = 3,
               format = "html")

	0.00054	0.00050	0.00047	0.00044
(Intercept)	7.037	7.038	7.038	7.039
Snp1	-0.937	-0.937	-0.937	-0.937
Snp2	0.217	0.218	0.218	0.218
Snp3	2.991	2.991	2.992	2.992
Snp4	0.193	0.193	0.193	0.193
Snp5	0.883	0.884	0.884	0.885
Snp6	-0.085	-0.085	-0.085	-0.085
Snp7	0.092	0.092	0.092	0.092
Snp8	0.000	0.000	0.000	0.000
Snp9	0.192	0.192	0.192	0.192

Note that for all values of \lambda, SNP 8 has \hat \beta = 0. This is because SNP 8 is a constant feature, a feature (i.e., a column of \mathbf{X}) whose values do not vary among the members of this population.

We can summarize our fit at the nth \lambda value:

# for n = 25 
summary(admix_fit, lambda = admix_fit$lambda[25])
#> lasso-penalized regression model with n=197, p=101 at lambda=0.08163
#> -------------------------------------------------
#> The model converged 
#> -------------------------------------------------
#> # of non-zero coefficients:  46 
#> -------------------------------------------------

We can also plot the path of the fit to see how model coefficients vary with \lambda:

plot(admix_fit)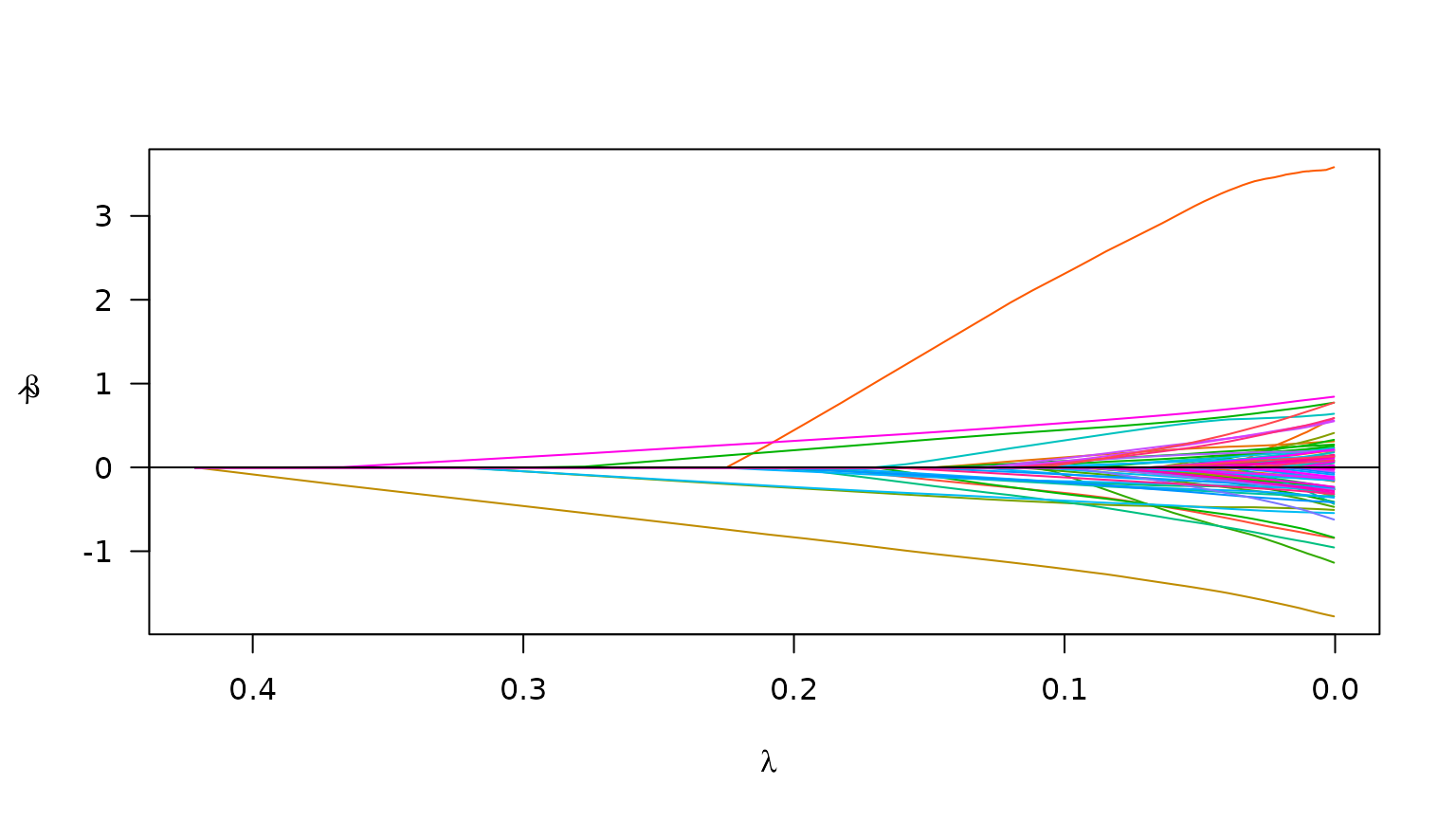

Plot of path for model fit

Suppose we also know the ancestry groups with which for each person in the admix data self-identified. We would probably want to include this in the model as an unpenalized covariate (i.e., we would want ‘ancestry’ to always be in the model). To specify an unpenalized covariate, we need to use the create_design() function prior to calling plmm(). Here is how that would look:

# add ancestry to design matrix
X_plus_ancestry <- cbind(admix$ancestry, admix$X)

# adjust column names -- need these for designating 'unpen' argument
colnames(X_plus_ancestry) <- c("ancestry", colnames(admix$X))

# create a design
admix_design2 <- create_design(X = X_plus_ancestry,
                               y = admix$y,
                               # below, I mark ancestry variable as unpenalized
                               # we want ancestry to always be in the model
                               unpen = "ancestry")

# now fit a model 
admix_fit2 <- plmm(design = admix_design2)

We may compare the results from the model which includes ‘ancestry’ to our first model:

summary(admix_fit2, idx = 25)
#> lasso-penalized regression model with n=197, p=102 at lambda=0.09886
#> -------------------------------------------------
#> The model converged 
#> -------------------------------------------------
#> # of non-zero coefficients:  14 
#> -------------------------------------------------
plot(admix_fit2)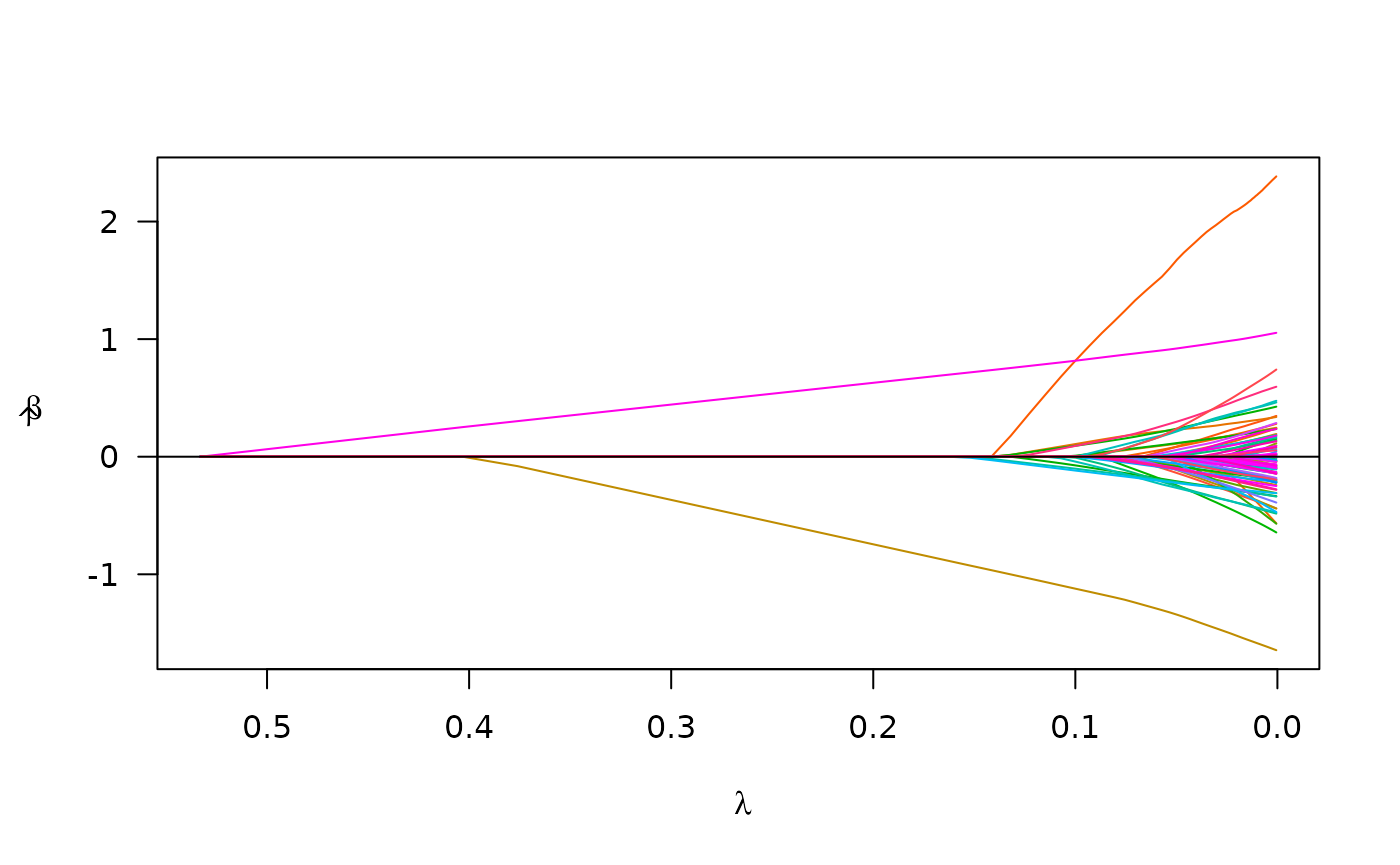

Cross validation

To select a \lambda value, we often use cross validation. Below is an example of using cv_plmm to select a \lambda that minimizes cross-validation error:


admix_cv <- cv_plmm(design = admix_design2, return_fit = T)

admix_cv_s <- summary(admix_cv, lambda = "min")
print(admix_cv_s)
#> lasso-penalized model with n=197 and p=102
#> At minimum cross-validation error (lambda=0.1853):
#> -------------------------------------------------
#>   Nonzero coefficients: 3
#>   Cross-validation error (deviance): 1.33
#>   Scale estimate (sigma): 1.154

We can also plot the cross-validation error (CVE) versus \lambda (on the log scale):

plot(admix_cv)

Plot of CVE

Parallelization

As an option for cross-validation, with data stored in-memory you may choose to implement CV in parallel using the cluster argument in cv_plmm(). Here is an example of setting up CV in parallel:

# make a cluster
num_cores <- 5 # just using 5 cores as a laptop-sized example
cl <- parallel::makeCluster(spec = num_cores)
print(cl) # check to see what kind of cluster you've made 
#> socket cluster with 5 nodes on host 'localhost'
cv_fit_parallel <- cv_plmm(design = admix_design2,
                           type = "blup",
                           cluster = cl,
                           return_fit = T,
                           trace = FALSE) 

# note: the results closely correspond to the above
summary(cv_fit_parallel)
#> lasso-penalized model with n=197 and p=102
#> At minimum cross-validation error (lambda=0.1853):
#> -------------------------------------------------
#>   Nonzero coefficients: 3
#>   Cross-validation error (deviance): 1.30
#>   Scale estimate (sigma): 1.138
plot(cv_fit_parallel)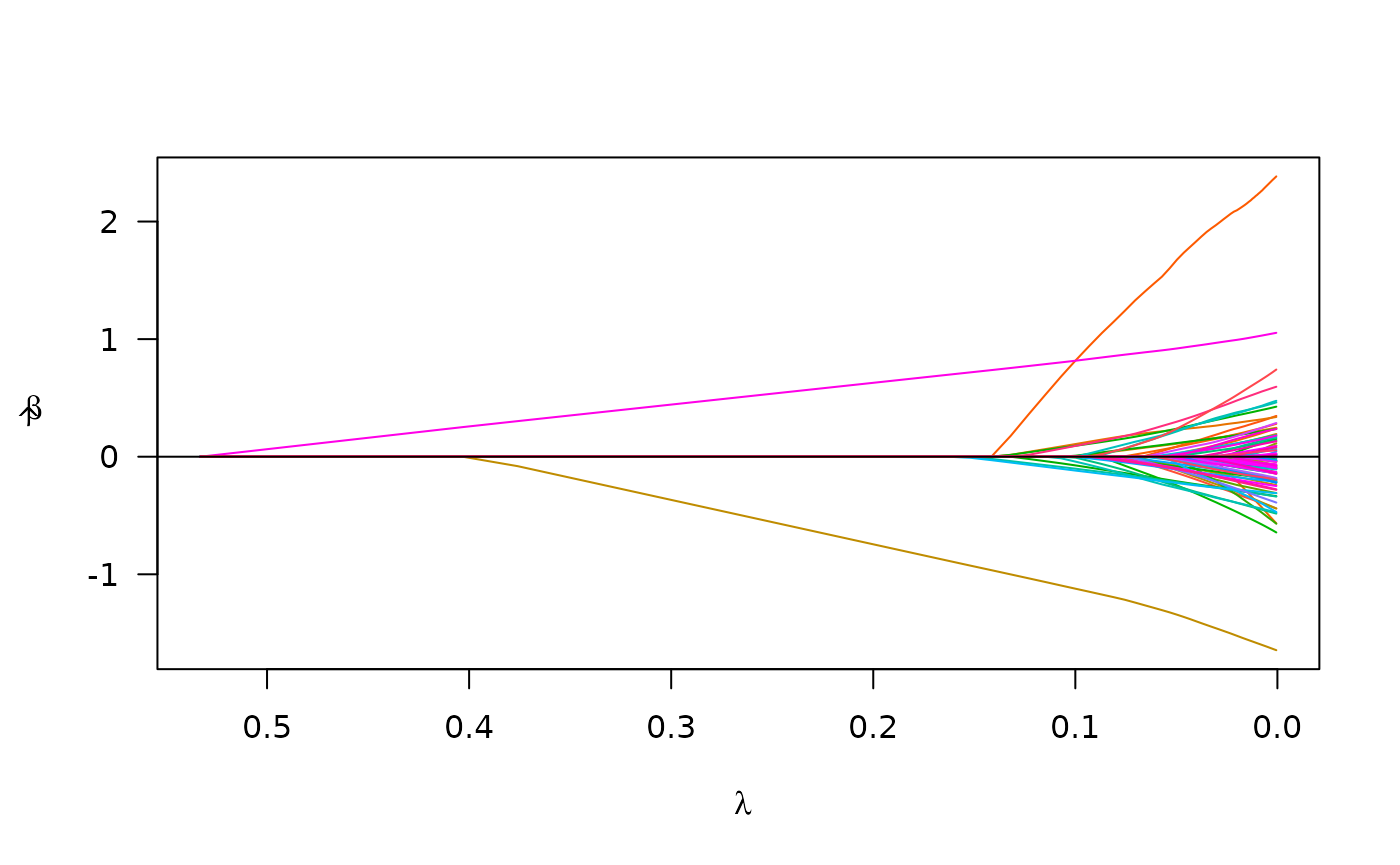

Prediction

Below is an example of the predict() methods for PLMMs:

# make predictions for select lambda value(s)
y_hat <- predict(object = admix_fit,
                 newX = admix$X,
                 type = "blup",
                 X = admix$X)

We can compare these predictions with the predictions we would get from an intercept-only model using mean squared prediction error (MSPE) – lower is better:

# intercept-only (or 'null') model
crossprod(admix$y - mean(admix$y))/length(admix$y)
#>          [,1]
#> [1,] 5.928528

# our model at its best value of lambda
apply(y_hat, 2, function(c){crossprod(admix$y - c)/length(c)}) -> mse
min(mse)
#> [1] 0.6930826
# ^ across all values of lambda, our model has MSPE lower than the null model

We see our model has better predictions than the null.